皆さんこんにちは! 数学塾講師のUKです。
今回扱う「正負の数」
という単元、これの特徴はなんと言っても、小学校六年間で出てこな
かった負の世界です。
しかし、この単元の理解が不十分だと中学数学は詰むといっても過言ではありません
今までに無いものが出てきたことで難しく感じる人もいますが蓋(ふ
た)を開けてみれば意外と簡単だったりします。
この記事では四則演算に重きをおいて進めていきます。
それではテストで80点以上とれるよう一緒に頑張りましょう!

「正負の数」の理解には数直線が必須!

正の数と負の数の違いは簡単に言うと 0より大きいか大きくないか、それだけです
数直線を使えばなにがわかりやすいかと言いますと、たくさんある中でもやはり「絶対値」と「数字の大小」です。
絶対値:数直線上の0からどれだけ離れているか。
数字の大小:数直線上で右にある数字ほど大きい
■「正負の数」の和と差
数直線の説明も終えたところで早速計算方法に入っていきましょう!
初めに言葉の説明に入らせていただきます。
これからの数学で知ってて当然の五つの単語です。
和:足し算
差:引き算
積:掛け算
商:割り算
四則:和・差・積・商をひとまとめにした呼び方
今あげた五つは必ず知っておいてください!
正負の和と差の計算では、
基本的にかっこがついた状態で問題に出てくることがほとんどです。
そのために「符号がぐちゃぐちゃになってしまう」なんて言うような経験もあると思います
しかし、かっこの外し方は意外にも超簡単なんです!
その方法は簡単に言うと
同じ符号は+
違う符号はー
文字の説明ではピンとこない人もいると思うので、こちらの画像を見てください!

この画像にもあるように注目してほしいのは真ん中とかっこを挟んで右側の符号です。
見ているだけよりも実際やってみたほうが力になると思うので和と差の練習問題を10問用意しました。
ぜひチャレンジしてみてください!
【問題】
1,(+7)+(-5) =
2,(-4)ー(-9) =
3,(-8)+(-12) =
4,(+15)ー(+20) =
5,(-6)ー(-3) =
6,(+18)+(-25) =
7,(-10)ー(+15) =
8,(-30)+(+45) =
9, -9+16 =
10, -20ー8 =【解答・解説】
1,(+7)+(−5)=+2
➡ 7−5=2。プラスが残る。
2,(−4)−(−9)=−4+9=+5
➡ マイナスを引くとプラス。
3,(−8)+(+12)=+4
➡ 12の方が大きいからプラス。
4,(+15)−(+20)=−5
➡ 15−20=−5。
5,(−6)−(−3)=−6+3=−3
➡「−(−)」は「+」に直す。
6,(+18)+(−25)=18-25=−7
➡ 25の方が大きいのでマイナス。
7,(−10)−(+15)=-10-15=−25
➡ マイナスの世界からさらに15下がる。
8,(−30)+(+45)=+15
➡ 45の方が大きいのでプラス。
9,−9+16=+7
➡ プラスの方が大きい。
10,−20−8=−28
➡ マイナス20からさらに8引くのでマイナス28。
さて、練習問題も終わり理解は進みましたか?
次は、正負の計算の積と商です。
■「正負の数」の積と商
和と差の説明も済んだところで積と商の説明をしていきたいのですが
積と商の計算をするとき気をつける符号の注意点はマイナスが式の中にいくつ出てきたのかというところです。
結論から申し上げると、
マイナスが偶数個(0,2,4,6,8…): プラス (+)
マイナスが奇数個(1,3,5,7,9…): マイナス(ー)
実はこれだけなんです!
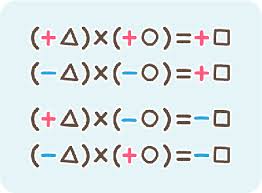
このように、マイナスが0個、1個の時はプラスになっていますし、 マイナスが1個の時はマイナスになっています。
それでは、練習問題にいってみましょう!
【問題】
1,(+3) × (+5) =
2,(-4) × (+6) =
3,(-7) × (-2) =
4,(+9) × (-8) =
5,(-5) × (+5) =
6,(-3) × (-7) × (-2) =
7,(-2) × (+4) × (-6) =
8,(-10) × (-6) =
9,(+24) ÷ (-6) =
10,(-36) ÷ (-9) =【解答・解説】
1,答え +15
解説 マイナスは0個(偶数) → 答えはプラス。
2,答え -24
解説 マイナスは1個(奇数) → 答えはマイナス。
3,答え +14
解説 マイナスは2個(偶数) → 答えはプラス。
4,答え -72
解説 マイナスは1個(奇数) → 答えはマイナス。
5,答え -25
解説 マイナスは1個(奇数) → 答えはマイナス。
6,答え -42
解説 マイナスは3個(偶数) → 答えはマイナス。
7,答え +48
解説 マイナスは2個(偶数) → 答えはプラス。
8,答え +60
解説 マイナスは2個(偶数) → 答えはプラス。
9,答え -4
解説 マイナスは1個(奇数) → 答えはマイナス。
10,答え +4
解説 マイナスは2個(偶数) → 答えはプラス。
■ まとめ
和と差
同じ符号:プラス + 違う符号:マイナスー
積と商
マイナスが偶数個:プラス + マイナスが奇数個:マイナスー
正負の数は符号のルールを覚えるのが鉄則!
逆を言えば、ルールさえ覚えれば正負の数の問題は小学校の知識で解けます!
そして、テストでは「符号ミス」、「絶対値」で必ず差がつきます!
なのでこの単元で高得点が取りたかったら、必ずたくさんの問題に触れてみてください!
そうすることで必然と正答率と解くスピードが伸びます!
それでは、皆さん勉強頑張ってください!!
